Дистанционно-векторный алгоритм при изменении стоимостей и неисправностях линий

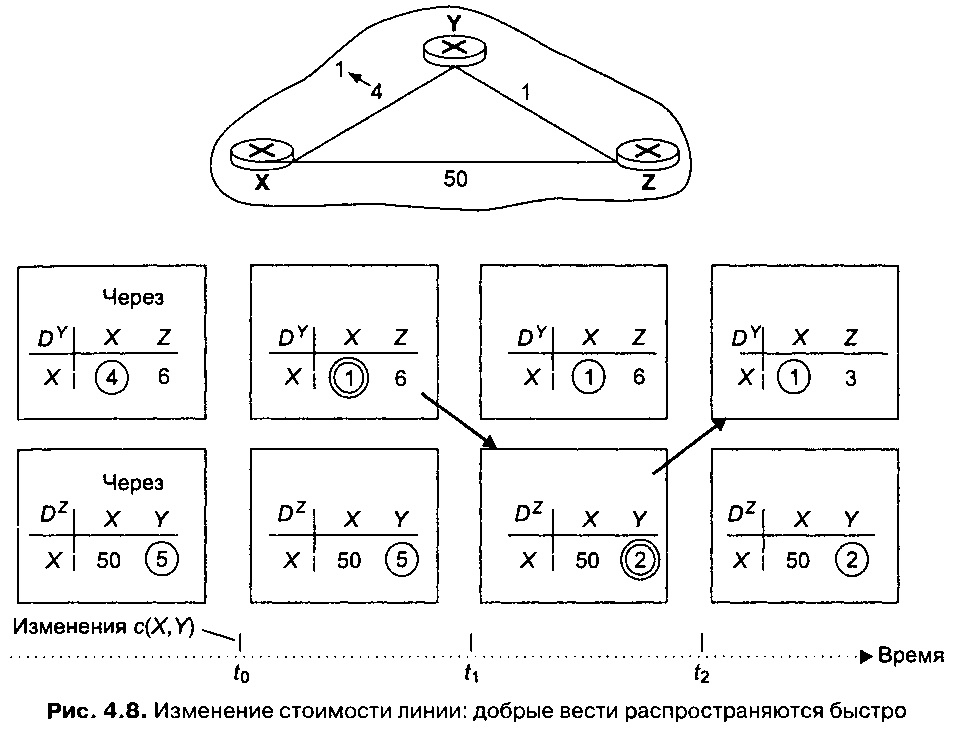
Когда узел, на котором работает дистанционно-векторный алгоритм, обнаруживает изменение стоимости линии, направляющейся от него к соседу (строка 12), он обновляет свою таблицу расстояний (строка 15) и, если наименьшая стоимость пути изменяется, он извещает об этом своих соседей (строки 23 и 24). Эту ситуацию иллюстрирует рис. 4.8. В данном примере стоимость линии от узла Xrq узла У изменяется с 4 до 1. Здесь мы рассматриваем только записи таблиц расстояний узлов У и Z, содержащие стоимости путей до узла X.

1. В момент времени t0 узел У замечает изменение стоимости линии (с 4 до 1) и информирует об этом своих соседей, так как благодаря изменению стоимости линии меняются минимальные стоимости путей.
2. В момент времени t1 узел Z получает сообщение от узла У и обновляет свою таблицу. Затем он вычисляет новое значение минимальной стоимости маршрута до узла X (она уменьшилась с 5 до 2) и извещает об этом своих соседей.
3. В момент времени t2 узел У получает сообщение от узла Z и обновляет свою таблицу. Его значения минимальных стоимостей не изменились (хотя стоимость пути до узла X через узел Z изменилась), поэтому узел Уне посылает сообщений своим соседям. Алгоритм переходит в стационарное состояние.

В примере на рис. 4.8 дистанционно-векторному алгоритму требуется только две итерации, чтобы перейти в стационарное состояние. «Хорошие новости» об изменившейся стоимости линии между узлами X и У быстро распространилась по сети.

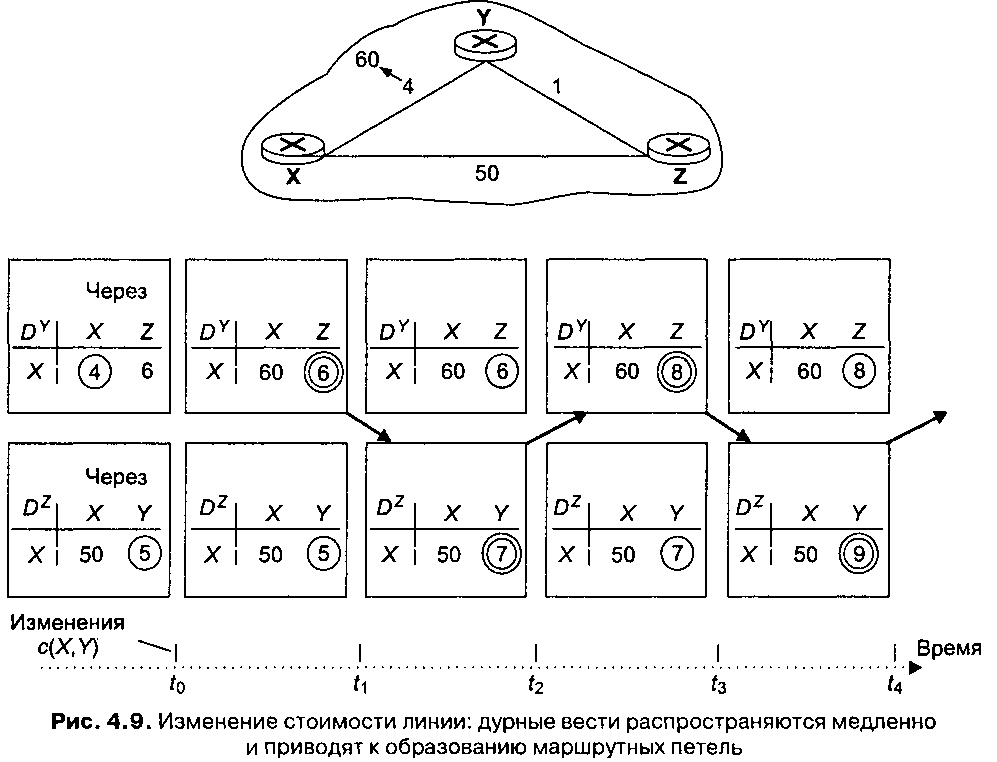
Рассмотрим теперь, что произойдет в случае увеличения стоимости линии. Предположим, что стоимость линии между узлами X и У возросла с 4 до 60, как показано на рис. 4.9.

1. В момент времени t0 узел У замечает изменение стоимости линии (с 4 до 60). Узел У вычисляет, что новая наименьшая стоимость пути до узла X равна 6. Этот путь проходит через узел Z. Поскольку мы можем видеть всю сеть сразу (глобально), нам понятно, что это новое значение неверно. Но узлу У известно лишь то, что стоимость его прямого соединения с узлом X равна 60 и что узел Z в последний раз сообщил узлу У, что у узла Zесть путь к узлу Xстоимостью 5. Узел У решает, что теперь ему дешевле посылать пакеты узлу X через узел Z. Таким образом, в момент времени tx у нас образовалась маршрутная петля — узел У направляет пакеты для узла X через узел Z, а узел Z направляет пакеты для узла X через узел У. Маршрутная петля подобна черной дыре — пакет, предназначенный узлу X, будет «отфутболиваться» узлами У и Z друг другу до тех пор, пока таблицы маршрутизации на этих узлах не изменятся.
2. Так как узел У вычислил новый путь наименьшей стоимости до узла X, он информирует об этом узел Z в момент времени t1.
3. Спустя некоторое время узел Z получает пакет с новой наименьшей стоимостью пути от узла У до узла X (узел У сообщил узлу Z, что новое значение наименьшей стоимости пути от узла У до узла X равно 6). Узел Z знает, что он может добраться до узла У по линии стоимости 1, и вычисляет новое значение стоимости маршрута до узла X (все также через узел У), равное 7. Поскольку наименьшая стоимость пути от узла Z до узла X увеличилась, узел Z извещает об этом узел Yb момент времени t2. 4.

Аналогичным образом узел Y обновляет свою таблицу и информирует узел Z о том, что новое значение минимальной стоимости равно 8. Затем узел Z обновляет свою таблицу и информирует узел Fo том, что новое значение минимальной стоимости равно 9, и т. д.

Как долго будет продолжаться этот процесс? Вы можете убедиться в том, что маршрутная петля будет сохраняться в течение 44 итераций (необходимых узлам 7и Zдля обмена сообщениями) — пока, наконец, узел Z не определит, что стоимость пути до узла X через узел Yбольше 50. В этот момент узел Z (наконец-то!) выяснит, что путь наименьшей стоимости к узлу X пролегает по прямой линии с узлом X. Таким образом, «дурным вестям» об увеличении стоимости линии между узлами Хи Гдля распространения по сети потребовалось очень много времени! Что бы произошло, если бы стоимость линии с( Y,X) увеличилась с 4 до 10 000, а стоимость линии c(Z,X) была бы равна 9999? Подобная проблема иногда называется проблемой «счета до бесконечности».