Циклический избыточный код
Широко применяемый в современных компьютерных сетях метод обнаружения ошибок основан на контроле при помощи циклического избыточного кода (Cyclic Redundancy Check, CRC). Циклические избыточные коды также называют полиномиальными кодами, так как при их вычислении битовая строка рассматривается как многочлен (полином), коэффициенты которого равны 0 или 1, и операции с этой битовой строкой можно интерпретировать как операции деления и умножения многочленов.
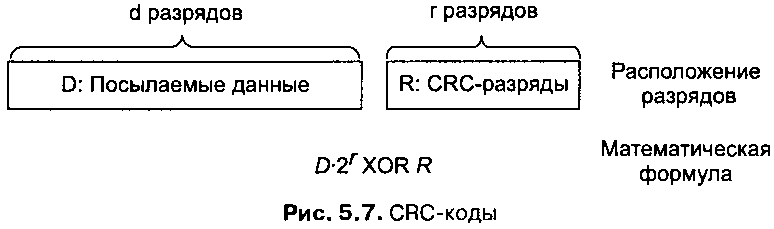
Циклические коды работают следующим образом. Рассмотрим фрагмент данных Д состоящий из d разрядов, которые передающий узел хочет отправить принимающему узлу. Отправитель и получатель должны договориться о последовательности из r+ 1 бит, называемой образующим многочленом (или генератором), который мы будем обозначать G. Старший (самый левый) бит образующего многочлена G должен быть равен 1. Ключевую идею циклических избыточных кодов иллюстрирует рис. 5.7. Для заданного фрагмента данных D отправитель формирует г дополнительных разрядов R, которые он добавляет к данным Д так что получающееся в результате число, состоящее из d + г бит, делится по модулю 2 на образующий многочлен (число) G без остатка. Таким образом, процесс проверки данных на наличие ошибки относительно прост. Получатель делит полученные d + г бит на образующий многочлен G. Если остаток от деления не равен нулю, это означает, что данные повреждены. В противном случае данные считаются верными и принимаются.
Все операции по вычислению CRC-кода производятся в арифметике по модулю 2 без переносов в соседние разряды. Это означает, что операции сложения и вычитания идентичны друг другу и эквивалентны поразрядной операции исключающего ИЛИ (exclusive OR, XOR). Например:
1011 XOR 0101 = 1110
1001 XOR 1101 = 0100
Также мы получим:
1011-0101 = 1110
1001-1101 = 0100
перации умножения и деления аналогичны соответствующим операциям в обычной двоичной арифметике с той разницей, что любая требующаяся при этом операция сложения или вычитания выполняется без переносов в соседний разряд. Как и в обычной арифметике, умножение на 2(k) означает сдвиг числа на k разрядов влево. Таким образом, при заданных значениях D и R величина D • 2(k) XOR R соответствует последовательности из d+ r бит, показанной на рис. 5.7. В нашем дальнейшем обсуждении мы будем использовать именно эту алгебраическую форму для обозначения последовательности из d + r бит.
Вернемся теперь к главному вопросу: как отправитель вычисляет R? Вспомним, что нам требуется найти такое значение R, чтобы для некоторого п выполнялось следующее равенство:
D•2(r) XOR R = nG.
То есть требуется выбрать такое значение R, чтобы D • 2(k) XOR R делилось на G без остатка. Если прибавить к каждой части уравнения значение R по модулю 2, то мы получим
D•2(r) = nG XOR R.
Отсюда следует, что если мы разделим D • 2(r) на G, то значение остатка будет равно R. Таким образом, мы можем вычислить R как
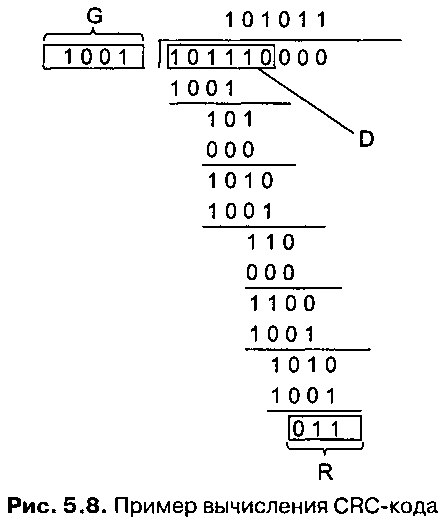
На рис. 5.8 показан пример вычисления R для D = 101110, d = 6, G = 1001 и r = 3. В этом случае отправитель передает следующие 9 бит: 1011100И. Вы можете сами проверить правильность расчетов, а также убедиться, что
D•2(r)-101011•2(r)=G XOR R.
Для 8-, 12-, 16- и 32-разрядных образующих многочленов определены международные стандарты. Восьмиразрядный CRC-код используется для защиты 5-байтового заголовка ATM-ячеек. В 32-разрядном стандарте CRC-32, принятом в ряде IEEE-протоколов канального уровня, используется образующий многочлен вида
G(crc-32) = 100000100110000010001110110110111.
Каждый стандарт CRC-кода способен обнаруживать ошибочные пакеты длиной не более г разрядов. Кроме того, при соответствующих допущениях ошибочный пакет длиной более чем г разрядов будет обнаружен с вероятностью 1 — 0,5Г. Помимо этого каждый стандарт CRC-кода может обнаруживать ошибки нечетной кратности.
Мой блог находят по следующим фразам