Алгоритм дистанционно-векторной маршрутизации
В отличие от алгоритма, основанного на состоянии линий и использующего глобальную информацию, дистанционно-векторный (Distance Vector, DV) алгоритм является распределенным, итерационным и асинхронным. Он является распределенным, так как каждый узел получает порцию информации от одного или нескольких напрямую соединенных с ним соседей, выполняет вычисления, а затем может разослать результаты своих вычислений своим соседям. Он является итерационным, так как этот процесс продолжается до тех пор, пока соседние узлы не перестанут обмениваться информацией. (Интересно отметить, что, как мы увидим, этот алгоритм сам завершает свою работу — он не получает «сигнала», требующего остановить работу; он просто останавливается.) Алгоритм является асинхронным, так как он не требует, чтобы все узлы работали в жесткой взаимосвязи друг с другом. Как мы увидим, асинхронный, итерационный, самоостанавливающийся, распределенный алгоритм значительно интереснее централизованного!
Главной структурой данных в дистанционно-векторном алгоритме является таблица расстояний, содержащаяся на каждом узле. В каждой таблице расстояний есть по строке для каждого адресата в сети и по столбцу для каждого ближайшего соседа. Рассмотрим узел X, который заинтересован в маршрутизации к адресату Y через ближайшего соседа Z. Запись в таблице расстояний Dx( YyZ) узла X представляет собой сумму стоимостей прямой линии между узлами X и Z, то есть c(X,Z) и известного на данный момент соседу Z пути наименьшей стоимости до узла У:
Второе слагаемое, минимальное значение стоимости пути, определяется по всем ближайшим соседям узла Z (включая, как мы скоро увидим, узел X).
Дистанционно-векторный алгоритм предполагает определенную форму общения между соседями — каждый узел должен знать наименьшую стоимость каждого пути от каждого из его соседей до каждого адресата. Таким образом, всегда, когда узел вычисляет новую минимальную стоимость до какого-либо узла, он должен сообщить об этом своим соседям.
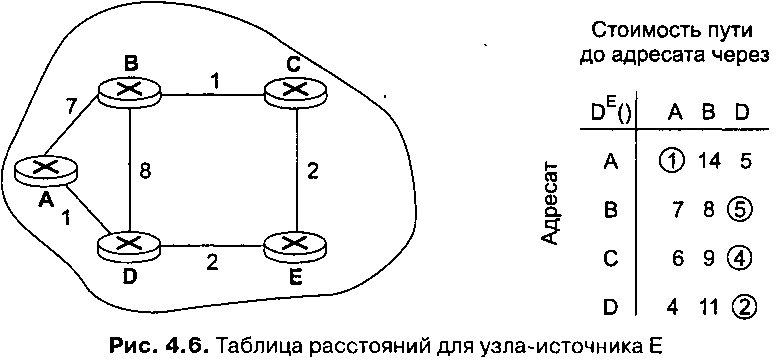
Прежде чем рассматривать дистанционно-векторный алгоритм, рассмотрим пример, который поможет нам понять смысл записей в таблице расстояний. Соответствующие топология сети и таблица расстояний для узла Е показаны на рис. 4.6. Эта таблица расстояний получена узлом Е после схождения алгоритма.
□ Обратите внимание на столбец для адресата А. Очевидно, путь с наименьшей стоимостью до узла Л идет по прямой линии, соединяющей узлы Ем А. Стоимость такого пути равна 1. Таким образом, DE(A,A) = 1.
□ Рассмотрим теперь значение DE(A,D) — стоимость пути от узла£ до узла Л, проходящего через узел D. В этом случае запись в таблице расстояний представляет собой стоимость пути от узла Е до узла D (2) плюс минимальную стоимость пути узла D до узла А. Обратите внимание, что минимальная стоимость пути узла D до узла А равна 3. Это путь, проходящий снова через узел Е! Тем не менее мы отмечаем, что минимальная стоимость пути от узла Е до узла Л, проходящего через узел Д равна 5. У нас, однако, остается подозрение,’что этот путь «зацикливается», проходя дважды через узел Е, и может стать источником проблем в дальнейшем.
□ Аналогично, мы можем определить, что стоимость пути от узла £ до узла Л, проходящего через узел В, равна 14. Обратите внимание, что стоимость этого пути равна именно 14, а не 15. (Почему?)
Кружками в таблице расстояний отмечены минимальные значения стоимости пути к данному адресату. Столбец с отмеченным кружком значением указывает следующий узел на пути с наименьшей стоимостью. Таким образом, из таблицы расстояний узла несложно построить таблицу продвижения данных (таблицу маршрутизации), в которой указывается, по какой линии следует посылать пакет каждому адресату.
Листинг 4.2. Дистанционно-векторный алгоритм (на каждом узле X)
1 инициализация:
2 для всех смежных узлов v:
3 Dx(*,v) = ∞ /* оператор * означает «для всех рядов» */
4 Dx(v,v) = c(X.v)
5 для всех адресатов, у
6 послать minJKy.w) каждому соседу /* w по всем соседям узла X */ 7
8 цикл
9 ждать (пока не изменится стоимость линии связи с соседом V
10 или пока не будет получено обновление от соседа V) 11
12 если (стоимость c(X.V) изменилась на d)
13 /* изменить стоимость путей ко всем адрсатам через соседа v на d */
14 /* величина d может быть положительной или отрицательной */
15 для всех адресатов у: Dx(y.V) = Dx(y.V) + d 16
17 иначе если (получено обновление от V, адресат Y)
18 /* изменился кратчайший путь от V до некторого Y */
19 /* Узел V послал свое новое значение minw Dv(Y.w) */
20 /* назовем это новое полученное значение «newval» */
21 для одного адресата у: DX(Y.V) = c(X.V) + newval
22
23 если мы получаем новое значение minw Dx(Y,w) для любого адресата Y
24 послать новое значение minw Dx(Y.w) всем соседям 25
26 конец цикла
При обсуждении записей таблицы расстояний узла Е мы рассмотрели сеть, для которой нам были известны стоимости всех линий. Дистанционно-векторный алгоритм, который мы сейчас рассмотрим, является децентрализованным и не пользуется подобной глобальной информацией. В самом деле, единственной информацией, которой обладает узел, являются стоимости линий, связывающих его с ближайшими соседями, а также сведения, получаемые им от этих ближайших соседей. Дистанционно-векторный алгоритм, который мы сейчас рассмотрим, также называют алгоритмом Беллмана-Форда, по именам его изобретателей. Он применяется на практике во многих протоколах маршрутизации, включая протоколы Интернета RIP и BGP, а также ISO IDRP, Novell IPX и оригинальный протокол сети ARPAnet.
Ключевыми являются строки 15 и 21 алгоритма, в которых узел обновляет свои записи в таблице расстояний либо в ответ на изменение стоимости присоединенной к узлу линии, либо в ответ на получение сообщения об обновлении от соседнего узла. Другим ключевым шагом является строка 24, в которой узел посылает обновленные данные своим соседям, если путь наименьшей стоимости до некоторого адресата изменился.
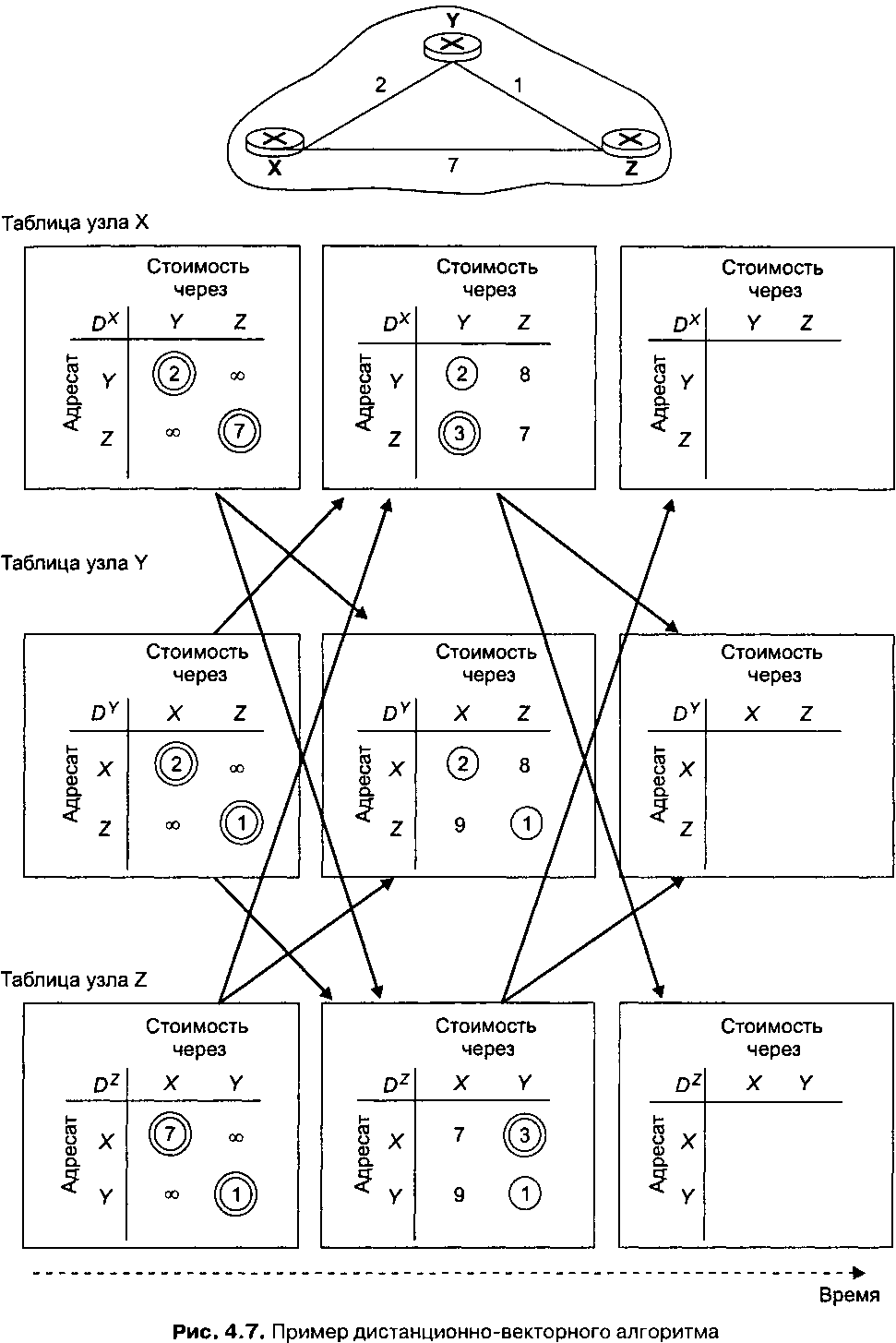
Рисунок 4.7 иллюстрирует работу дистанционно-векторного алгоритма для простой сети из трех узлов, изображенной в верхней части рисунка. Алгоритм функционирует синхронно, то есть все узлы одновременно получают сообщения от своих соседей, .вычисляют новые значения записей таблицы расстояний и информируют своих соседей о любых изменениях в их путях с наименьшей стоимостью. Когда вы изучите этот пример, вам придется поверить, что данный алгоритм столь же корректно работает и в асинхронном режиме, когда производимые узлами вычисления и обмен данными между узлами происходят в произвольные моменты времени. Обведенные кружками записи в таблицах расстояний на рисунке показывают текущие минимальные значения стоимости пути до адресата. Запись, обведенная двойным кружком, означает, что была вычислена новая минимальная стоимость (в строке 4, 15 или 21 дистанционно-векторного алгоритма). Те случаи, когда соседям посылается сообщение об изменении стоимости (строка 24 дистанционно-векторного алгоритма), отмечены на рисунке стрелками. В самом левом столбце на рисунке показаны записи таблиц расстояний для узлов X, Y и Z после первого шага инициализации.
Рассмотрим теперь, как узел X вычисляет таблицу расстояний, показанную в средней колонке, после получения обновлений от узлов Ки Z. Получив обновления от узлов Yn Z, узел X выполняет строку 21 дистанционно-векторного алгоритма:
Важно отметить, что узел X узнает о значениях min^ Dz( Y,w) и min^ DY(Z,w) только потому, что узлы У и Z посылают ему эти значения (их узел X получает в строке 10 дистанционно-векторного алгоритма). В качестве упражнения проверьте таблицы расстояний, вычисленные узлами Уи Zb средней колонке (см. рис. 4.7).
Значение DX(Z,Y) = 3 во второй таблице расстояний узла Xозначает, что наименьшая стоимость пути от узла X до узла Zизменилась с 7 до 3. Таким образом, узел X посылает новое значение стоимости пути до узла Z узлам У и Z, информируя их об этом. Обратите внимание, что узлу Хне нужно посылать обновления узлам Уи Z о стоимости пути к узлу У, так как она не изменилась. Также обратите внимание, что хотя в результате новых расчетов узел У получает новые значения элементов таблицы расстояний, значения минимальных стоимостей путей к узлам X и Z не изменяются. Поэтому узел Уне посылает обновлений узлам X и Z.
Процесс получения от соседей новой информации о стоимости путей, вычисления новых табличных значений и извещения своих соседей об изменениях в стоимости путей продолжается до тех пор, пока стоимости не перестанут изменяться. С этого момента алгоритм становится статическим, поскольку сообщения с новыми значениями более не посылаются и значения в таблице не пересчитыва-ются; то есть все узлы переходят в состояние ожидания в строке 9. Алгоритм остается в статическом состоянии до тех пор, пока стоимость какой-либо линии не изменится.
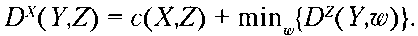
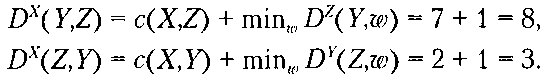
Прекрасная статья, спасибо. Всё понятно и подробно объяснено, я как раз такое искал.