Задержка ожидания d(ожид)
Наиболее сложным и интересным видом задержек, возникающих при передаче пакетов, является задержка ожидания d(ожид). Эта величина имеет настолько важное значение для сетевых технологий, что ей посвящены десятки книг и сотни научных статей. Сейчас мы не будем излишне углубляться в теорию массового обслуживания и рассмотрим задержку ожидания и ее последствия лишь в общем плане.
Задержка ожидания — единственная составляющая узловой задержки, которая может иметь разные значения для разных пакетов. Так, например, если в изначально пустой буфер маршрутизатора одновременно поступит 10 пакетов, то задержка ожидания для первого пакета будет равна нулю, а для последнего пакета она окажется равной времени, необходимому для обслуживания девяти предыдущих пакетов. Таким образом, значение задержки ожидания является случайным, и для его оценки необходимо использовать статистические величины: среднее время ожидания, дисперсию времени ожидания и вероятность превышения временем ожидания заданной величины.
Каковы факторы, влияющие на величину задержки ожидания? Можно выделить три из них: частоту получения пакетов, скорость передачи выходной линии связи и закон распределения получаемых пакетов во времени. Последний характеризует, является ли получение пакетов периодическим или апериодическим. Пусть а — средняя частота получения пакетов, измеряемая в пакетах в секунду, R — скорость передачи по выходной линии связи в битах в секунду, a L — длина пакета в битах. Тогда скорость получения данных маршрутизатором равна L x a бит/с. Предположим, что буфер маршрутизатора является бесконечно большим, то есть позволяет организовать очередь бесконечной длины. Величина L х a/R, называемая интенсивностью трафика, играет определяющую роль в оценке длины очереди. Если L х a/R > 1, то средняя скорость приема информации превышает среднюю скорость ее передачи, что приводит к неограниченному росту очереди. Отсюда вытекает «золотое правило» организации трафика: обмен информацией всегда должен быть организован так, чтобы интенсивность трафика не превышала 1. Далее будем считать, что L x a/R<=l.
При отсутствии перегрузок можно исследовать влияние интенсивности трафика на величину задержки ожидания. Если появление новых пакетов происходит периодически, например каждые L/R секунд, то каждый пакет будет приходить в пустой буфер, и, следовательно, время ожидания окажется равным нулю. Если новые пакеты появляются периодически, но не поодиночке, то среднее время ожидания для них, очевидно, уже не будет нулевым. Пусть каждые (L/R) х N секунд происходит появление N пакетов, тогда для первого пакета время ожидания будет равно 0 с, для второго пакета — L/R с, а для n-го пакета — (n — 1) х L/R с. Среднее время ожидания для этого случая мы предлагаем вам подсчитать самостоятельно в качестве упражнения.
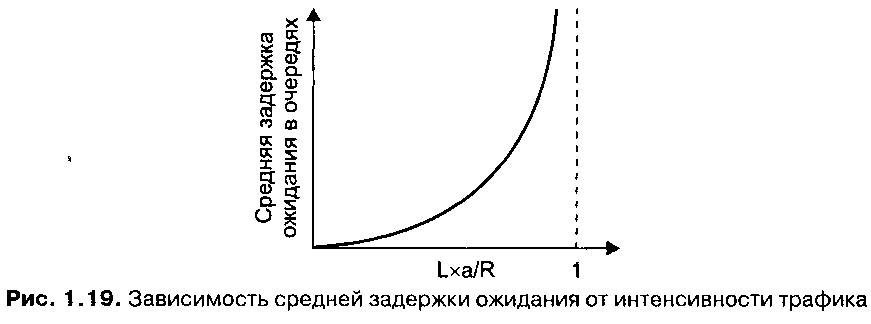
Оба рассмотренных примера являются скорее теоретическими, чем практическими. На практике типично появление пакетов в случайные моменты времени. Другими словами, момент появления нового пакета, а следовательно, и время между появлениями соседних пакетов, нельзя предсказать заранее. В этом случае значение интенсивности трафика не дает точного ответа на вопрос о величине задержки ожидания. Тем не менее интенсивность способна наглядно проиллюстрировать зависимость задержки ожидания от соотношения скоростей приема и передачи пакетов. Если интенсивность трафика близка к нулю, то, очевидно, вероятность непустого буфера в момент получения нового пакета мала, и поэтому среднее время ожидания также близко к нулю. Если же интенсивность имеет значение, близкое к единице, то возможны кратковременные превышения скорости приема над скоростью передачи и, как следствие, появление очередей и увеличение их длины. Чем ближе к единице значение интенсивности трафика, тем выше вероятность увеличения очереди и времени ожидания. На рис. 1.19 зависимость между интенсивностью и временем ожидания представлена графически.
Как видно из рисунка, в области интенсивностей, близких к 1, даже небольшой прирост интенсивности влечет за собой значительно больший прирост задержки ожидания. Этот математический эффект легко проиллюстрировать с помощью примера. Когда вы движетесь по трассе, которая до отказа заполнена машинами, даже самое незначительное снижение пропускной способности трассы (то есть увеличение интенсивности) влечет за собой длительные автомобильные «пробки».